Evaluation of Mass Transfer Coefficient in a wetted wall column
Objective: The rates of diffusion into gases flowing through pipes are studied in wetted wall column.
Principle/Theory:
A thin film of liquid falling down inside of a vertical pipe through which the gas flows constitutes a wetted wall column. Wetted wall columns have been used as Hydrochloric acid, Ammonia, Acetone, Benzene and other volatile liquids absorbers. They have also been studied for theoretical studies for mass transfer because the interfacial surface between the phases is kept under control and is measurable.
The height of the wetted wall column required for mass transfer operations is excessive and consequently, this is not widely used, where large quantities of liquid or gas have to be handled, it would be necessary to arrange many vertical pipes in parallel and this leads to difficulties in the distribution of liquid into the inner surface of the tubes. The gas pressure drop for this is confined to skin friction effects, with few or no expansion or contraction losses
.
.
The rates of diffusion into gases flowing through pipes have been studied in wetted wall columns.
A volatile liquid is submitted to flow down the inside surface of a circular tube, while a gas flows upward or downward through the center of the pipe. Measurement of the rate of evaporation of a liquid into the gas stream over a known surface permits calculation of the mass transfer coefficient for the diffusion of vapor into the gas stream. Since the liquid is pure, the concentration gradient for diffusion exists entirely within the gas phase, the mass transfer coefficient Kg may be calculated. Sherwood and Gillard conducted a series of experiments using a variety of volatile liquids with air in turbulent flow.
The equation which describes all the data for both liquid and gas flow is
(KG d/DW (PBM/P) (Kld/D) = 0.023 Re0.83 Sc1/3
This empirical relation is quite remarkable in the manner in which it generally confirms the relationship between heat mass and momentum transfer developed theoretically. However, the evaporation of the volatile liquids in a wetted wall column results in the cooling of the liquids and consequent simultaneous heat transfer between liquid and gas. The heat transfer rates are given by the equation
hd / k = 0.023 Re0.8 Pr0.3
Equipment used: Wetted Wall column unit, Humidity meter
The material used: Water
EXPERIMENTAL PROCEDURE:
EXPERIMENTAL PROCEDURE:
2. The blower is started and the minimum flow of air is maintained.
3. After about 5 minutes, when steady-state conditions reach, the humidity of air at the inlet and outlet is determined by the readings of the wet and dry bulb thermometers and by the use of a psychometric chart.
4. Water flow rates and inlet and outlet temperatures are noted.
5. The vapor pressure of water at different water temperatures is calculated.
6. Calculations are made at different flow rates and values of Kg Vs NRe are plotted on a log-log scale.
Here are the details of the observation table and the calculation format for your reference.
Here are the details of the observation table and the calculation format for your reference.
OBSERVATIONS:
S.No
|
Air flow rate from M2 Qa lpm
|
Water flow rate Qw lpm
|
Air temperature
|
Water temperature 0C
|
Air PD mm H20 across the orifice
| |
Inlet
|
Outlet
|
T1 T2
|
M1 M2
| |||
Td1tw1
|
Td2 tw2
| |||||
1
| ||||||
2
| ||||||
Length of the tube =
Diameter of tube =
From the readings, Td1, tw1 and Td2 , tw2 and from a psychometric chart,
Partial pressure of water vapor at inlet = P1 KN/m2
Partial pressure of water at outlet = PB KN/m2
DATA ANALYSIS:Partial pressure of water at outlet = PB KN/m2
Mean air pressure in column Pt = PB *(DP1/2)X1000/13600*1.013*100/760 KN/m2
9.22 X SQRTDP2/106 kgmoles/sec
Driving force at inlet of air= DpW1 = PW1 –pw1
Where,
pw1 =pure component vapour pressure of water at outlet water temp T1
PW1 = Partial pressure of water at the bottom
Driving force at the outlet of the air
DpW1 = PW2 –pw2
where,
pw1 =pure component vapor pressure of water at outlet water temp T2
PW2= Partial pressure of water at the top of the column
DPwm = (DpW1 - DpW2)/ ln (DpW1/DpW2)
Amount of water evaporated
NW = QA* (pw2/Pt – pw1/Pt)
In terms of mass transfer coefficient Kg, the rate of mass transfer is given by
Nw = KG * A* DPwm
where A = p DL m2 where d = i.d of column and L = Effective length of column
For each flow rate of air ,Kg can be calculated.
Pam = (Pt – pw1) – (Pt –Pw2)/ ln (Pt – pw1/ Pt –Pw2) is also calculated
To plot Gillard correlation, Kg * (d/DW)* (Pam/Pt) * (rADw/mair) 0.44
Where Dw = diffusivity of water vapor in air = 0.13X10-4 m2/sec
mair =viscosity of air = 1.85X 10-3 kg/m/sec
Nre = dG/ mair = d.QA.AC/mair
Ac =cross section area of column
d = diameter of column
Kg * (d/DW)* (Pam/Pt) * (rADw/mair) 0.44 Vs Nre is plotted on a log –log sclae.
This value is compared with reported values.
RESULTS:
Reported value =
Calculated value =
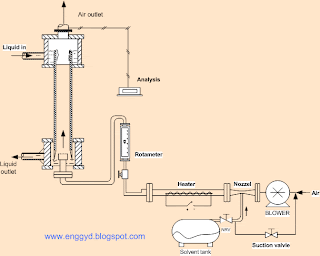 |
| Wetted Wall Column Set Up |
The above setup is used to calculate the experimental mass transfer coefficient of the liquid and gas system at different temperatures and different flow rates; of course, the main application of the wetted wall is to determine the data of the gas and liquid mass transfer coefficient.
A blower is provided with two valves at suction so that when the studies are focused on vapors of a chemical substance that are stored in a storage vessel and the vapors from the vessel are sucked by the blower and passed into the column or if the vapors are required to be mixed with air than an option at the discharge line of the blower which is facilitated with nozzle helps in mixing the vapor with air.
A heater is provided at the discharge line to supply heat to the vapor or air to maintain the temperature of the system and the whole pipeline is insulated to prevent loss, by using the rotameter, the flow rate of the vapor can be controlled.
 |
| PSYCHROMETRIC CHARTS |
Application of wetted wall column:
 |
| Wetted wall column equipment, industrial application |
The Heart of Thermal Phosphoric Acid Production: Wetted Wall Column Technology
Thermal phosphoric acid production relies on a pivotal component: the combustion chamber, intricately designed and integrated with a wetted wall column. This innovative setup facilitates the transformation of phosphorus into phosphoric acid, a crucial process in various industries.
The Wetted Wall Column: A Masterpiece of Engineering
The column's clever design enables efficient phosphoric acid production. Here's how it works:
Step-by-Step Process
1. Combustion Chamber: Phosphorus and air ignite, producing a hot gas mixture.
2. Column Inlet: The combusted mixture enters the top of the column.
3. Water Flow: A thin film of water cascades down the column's walls.
4. Reaction Zone: Phosphorus pentoxide reacts with water, forming phosphoric acid (H3PO4).
5. Product Collection: The resulting phosphoric acid collects at the column's base.
Key Benefits
1. Efficient heat transfer and reaction rate optimization.
2. Minimal energy consumption.
3. High-purity phosphoric acid production.
4. Compact design, reducing spatial requirements.
The Science Behind the Process
Phosphorus pentoxide (P2O5) reacts with water (H2O) to form phosphoric acid:
P2O5 + 3H2O → 2H3PO4 (Hydration reaction of phosphorus pentoxide)
Industrial Applications
1. Fertilizer production.
2. Pharmaceutical manufacturing.
3. Food processing.
4. Detergent industry.
The wetted wall column is the linchpin of thermal phosphoric acid production. Its ingenious design ensures efficient, high-quality acid production, making it an essential component in various industries